Dagens tekst er hentet fra kapittel 4 i Cryptography and Network Security. Dette kapitlet skal se nærmere på moderne blokk-chiffre, som er av de mest brukte kryptografiske algoritmene for hemmelighold og autentisering. Som et konkret eksempel vil vi studere DES-algoritmen for å illustrere designprinsipper for blokkchiffer.

Blokkchiffer kontra flytchiffer

Blokkchiffre prosesserer meldinger i blokker som individuelt krypteres/dekrypteres. Dette kan nesten sammenlignes med substitusjon av veldig store bokstaver. Blokkstørrelsen er typisk 64 bit eller mer (senere år er 128 bit mer vanlig). Flytchiffer prosesserer meldinger en bit eller byte om gangen når de krypterer eller dekrypterer. Mange av krypteringsalgoritmene som brukes i dag er blokkchiffre, derfor er disse ofte grundigere analysert, og har et bredere anvendelsesområde.

Flytchiffer

Eksempler på flytchiffer omfatter Autokeyed Vigenère og Vernam. I det ideelle tilfellet vil en one-time pad versjon av Vernam chifferet brukes, hvor nøkkelstrømmen er like lang som klartekst-bitstrømmen. Hvis den kryptografiske nøkkelstrømmen er tilfeldig er dette chifferet umulig å knekke på annet vie en å finne nøkkelstrømmen. Nøkkelstrømmen må gjøres tilgjengelig for begge parter (avsender og mottaker) via en uavhengig og sikker kanal. Logistikkmessig kan dette representere bortimot uoverstigelige problemer hvis den tiltenkte datatrafikken er veldig stor. Av praktiske årsaker må derfor bitstrømmen implementeres som en algoritmisk prosedyre slik at den kan produseres parallelt av begge partene. For at dette skal være sikkert må det være beregningsmessig upraktisk (“umulig”) å forutse fremtidige deler av bitstrømmen basert på deler som allerede har blitt brukt. De to partene må bare dele den genererende nøkkelen på ett eller annet vis, og kan deretter begge produsere nøkkelstrømmen.

Blokkchiffer

En blokk med klartekst behandles som en helhet, og brukes til å produsere en blokk chiffertekst av samme lengde, typisk 64 eller 128 bit. På samme måte som ved et flytchiffer, så deler de to partene en symmetrisk krypteringsnøkkel. De fleste av dagens nettverksbaserte symmetriske krypteringsapplikasjoner bruker blokkchiffer.

Prinsipper for blokkchiffer

De fleste symmetriske blokkchiffer er basert på en såkalt Feistel-struktur. Dette er nødvendig for å kunne dekryptere melding på en effektiv måte. Som sagt kan vi se på et blokkchiffer som en veldig stor substitusjonsoperasjon. Skulle vi ha laget en tabell for dette, ville vi ha trengt 264 innslag for en 64-bits blokk, så i stedet konstrueres chifferet fra mindre byggesteiner etter ideen om et produkt-chiffer.

Claude Shannon og Substitusjon-Permutasjon chiffer

Claude Shannon, informasjonsteoriens far, introduserte ideen om substitusjon-permutation (S-P) nettverk i 1949. Disse danner grunnlaget for moderne blokkchiffer. S-P nettverk er basert på de to primitive kryptografiske operasjonene vi allerede har diskutert: substitusjon (S-box) og permutasjon (P-box). Disse gir oss forvirring (confusion) og diffusjon av melding og nøkkel.

Diffusjon og forvirring

Disse begrepene ble introdusert av Shannon for å fange de to grunnleggende byggesteinene for ethvert kryptografisk system. Det Shannon var opptatt av, var å forhindre kryptoanalyse basert på statistisk analyse.

Diffusjon betyr at den statistiske strukturen av klarteksten spres ut til langttrekkende statistiske egenskaper i chifferteksten. Dette oppnås ved å sørge for at hvert tegn i klarteksten påvirke verdien til mange tegn i chifferteksten.

Forvirring (confusion) søker å gjøre forholdet mellom statistikken til chifferteksten og verdien av krypteringsnøkkelen så kompleks som mulig. Selv om angriperen skulle klare å danne seg et bilde av de statistiske egenskapene til chifferteksten, skal måten nøkkelen ble brukt til å lage denne chifferteksten være så kompleks at det er vanskelig å dedusere nøkkelen.

Feistel-chiffer

Shannons ideer om et produkt-chiffer som kombinerer forvirrings- og diffusjons-funksjoner ble implementert i praksis av tyskfødte Horst Feistel, ved å alternere substitusjoner og permutasjoner.

Substitusjon: Hvert klartekst element eller gruppe av elementer er unikt byttet ut med et korresponderende chiffertekst-element eller gruppe av elementer.

Permutasjon: Ingen elementer legges til eller fjernes fra sekvensen, men i stedet endres rekkefølgen som elementene opptrer i sekvensen.

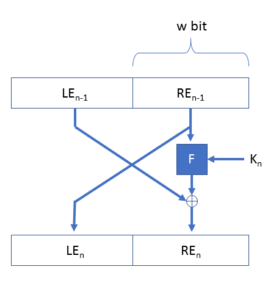
Et Feistel-chiffer har en blokkstørrelse på 2w bit, og består av n runder hvor to halvparter av blokken behandles hver for seg. Nøkkelen K deles opp i et sett undernøkler K₁, K₂, … K_n, som hver består av y bit. En enkelt runde ser ut som vist på bildet til høyre.

En interessant egenskap er at dekryptering i prinsippet er det samme som kryptering, bare at subnøklene brukes i motsatt rekkefølge.

Feistel designkriterier

Større blokkstørrelse og lengre nøkler gir begge hver for seg bedre sikkerhet, men redusert krypterings-/dekrypteringshastighet for en gitt algoritme. En vesentlig ting med et Feistel-chiffer er at en enkelt runde ikke gir tilstrekkelig sikkerhet, men sikkerheten øker med hver runde (men det gjør også prosesseringstiden). Mer kompleksitet i algoritmen som genererer subnøklene skal føre til større utfordringer for kryptoanalyse. Det samme gjelder rundefunksjonen F, dess mer kompleks den er, dess generelt større motstandsdyktighet mot kryptoanalyse.

Hvis krypteringsfunksjonen er innebygget i applikasjoner eller funksjoner på en slik måte at en maskinvareimplementasjon er utelukket vil utførelseshastigheten være noe man må bekymre seg om.

Til slutt, hvis algoritmen kan beskrives på en kortfattet måte og forklares godt, vil den være lettere å analysere for å finne eventuelle kryptoanalytiske sårbarheter, og det vil derfor være mulig å oppnå større tiltro til styrken av den.

Historien til Data Encryption Standard (DES)

En gruppe hos IBM under ledelse av Feistel utviklet et chiffer kalt Lucifer på slutten av 60-tallet. Lucifer hadde 64-bits blokkstørrelse og opp til 128-bit nøkkel. Dette ble så videreutviklet til et kommersielt chiffer med innspill fra NSA og andre. I 1973 inviterte National Bureau of Standards (NBS) til forslag for en ny nasjonal chifferstandard. IBM sendte inn deres reviderte Lucifer som til slutt ble akseptert som DES; standarden ble utstedt i 1977 av NBS (nå NIST) som Federal Information Processing Standard (FIPS) 46. DES var det hyppigst brukte krypteringssystemet fram til introdusjosnen av Advanced Encryption Standard (AES) i 2001.

Selve algoritmen skal egentlig kalles Data Encryption Algorithm (DEA) – men det er det de færreste som har gjort. Data krypteres i 64-bit blokker vha. en 56-bit nøkkel, algoritmen transformerer altså 64-bit input gjennom en serie av steg til 64-bit output. De samme stegene, med samme nøkkel brukes til å reversere krypteringen – men nøkkelen behandles litt ulikt internt.

Kontroverser rundt DES

Selv om Data Encryption Standard er offentlig, var det betydelige kontroverser rundt designet til DES. Spørsmål ble reist rundt valget av en 56-bit nøkkel (jfr. Lucifer 128-bit), og det at designkriteriene var hemmelige, men senere hendelser og offentlig analyse har vist at designet faktisk var hensiktsmessig. Bruken av DES har vært utstrakt, spesielt i finansielle applikasjoner. Den brukes fortsatt i enkelte eldre applikasjoner.

DES detaljer

Initiell permutasjon (IP)

Det første steget i krypteringen stokker om på rekkefølgene av input bit – dette kalles den initielle permutasjonen (IP). Fiffig nok ordnes det slik at heltalls bit havner i den venstre halvdelen (LH), mens oddetalls bit havner i den høyre halvdelen (RH). Denne strukturen er ganske regelmessig, noe som gjør det enkelt å implementere både i maskinvare og programvare. Eksempel:

IP(675a6967 5e5a6b5a) = (ffb2194d 004df6fb)

DES rundestruktur

DES bruker to 32-bit L & R halvparter, og som ethvert Feistel-chiffer kan vi utrykke dette som :

L_i = R_i–1

R_i = L_i–1 ⊕ F(R_i–1, K_i)

Rundefunksjonen F mates med den 32-bit R halvparten og en 48-bit subnøkkel, ekspanderer R til 48-bits vha. permutasjon E, legger til subnøkkelen vha using XOR, og sender resultatet på 48 bit gjennom 8 S-bokser for å få et 32-bit resultat. Det hele permuteres til slutt vha. 32-bit permutasjon P.

Substitusjonsbokser S

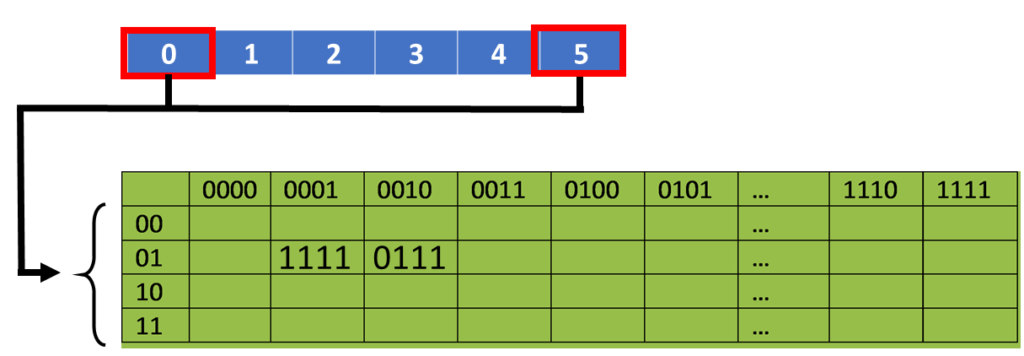
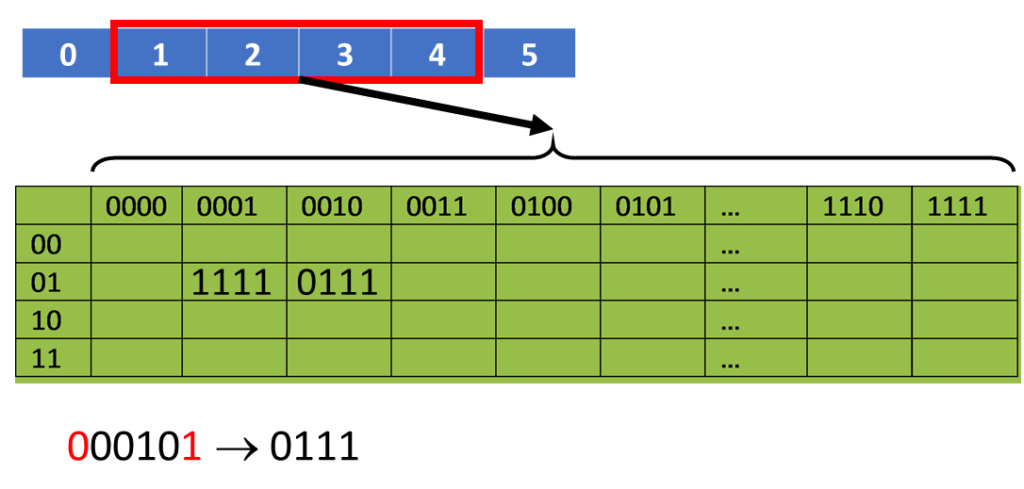
Funksjonen F inneholder åtte S-bokser som avbilder 6 til 4 bits. Det går an å se på hver S-boks som fire små 4 bit bokser (4 rader). De ytre bitene (1 & 6) velger en av de fire radene, mens de indre 4 bits (2-5) velger en kolonne (se illustrasjonen under). Vi ender opp med 8 grupper á 4 bit, tilsammen 32 bit. Ettersom valget av rad og kolonne avhenger av både klartekst og data, har vi en egenskap kalt “autoklaving” (eller autokeying). Eksempel: S(18 09 12 3d 11 17 38 39) = 5fd25e03

DES nøkkelplan (key schedule)

Nøkkelplanen danner subnøklene som brukes i hver runde. Den første permutasjonen av nøkkelen (PC1) velger de 56 signifikante bits i to 28-bit halvparter. Man går deretter gjennom 16 runder som består av å rotere hver halvpart hver for seg enten en eller to plasser (bit) avhengig av nøkkelrotasjonsplanen K, og deretter velge 24 bits fra hver halvpart og permutere dem med PC2 for å mates inn i rundefunksjonen F.

DES dekryptering

Dekryptering må “gjøre ommat” alle operasjonene gjort i krypteringen. Med et Feistel design, gjør man krypteringsstegene om igjen med subnøklene i omvendt rekkefølge (SK16 … SK1). IP er den omvendte operasjonen av det siste steget av krypteringen (FP). Den første runden med SK16 opphever den 16nde krypteringsrunden, … , den 16nde runden med SK1 opphever den første krypteringsrunden, og til slutt opphever FP den initielle permuteringen IP, slik at vi er tilbake til den opprinnelige klarteksten.

Skredeffekten

Den såkalte skredeffekten (avalanche effect) er en sentral ønskelig egenskap til en krypteringsalgoritme; en endring i 1 bit i input eller nøkkel skal resultere i at omtrent halvparten av bitene i resultatet endres. Dette gjør det umulig å gjette nøkkel ved “innsirkling”. DES har sterk skred-effekt.

DES designkriterier

For noen år siden løftet Coppersmith litt på sløret som har skjult designkriteriene for DES. Det er 7 kriterier for S-bokser som gir ikke-lineære egenskaper, motstansdyktighet mot differensiell kryptoanalyse og god forvirring (confusion). Det er tre kriterier for permutasjonen P som gir økt diffusjon.

DES styrke

Det finnes tidsbaserte angrep (Timing attacks) mot kryptosystemer hvor informasjon om nøkkel eller klartekst kan finnes ved å observere hvor lang tid en gitt implementasjon trenger for å utføre dekryptering på forskjellige chiffertekster. Disse utnytter det faktum at en krypterings- eller dekrypteringsalgoritme ofte trenger ørlite forskjellig tid på å behandle forskjellig input.Så langt ser det usannsynlig ut at denne teknikken noensinne kommer til å bli effektiv mot DES eller kraftigere symmetriske chifre som AES.

Det finnes i dag flere analytiske angrep mot DES, som utnytter den dypere strukturen til chifferet ved å samle informasjon om krypteringer. Kan til slutt avdekke noen/alle bits i subnøkkelen, og om nødvendig foreta et uttømmende søk for de gjenværende. Disse er generelt sett alle statistiske angrep som differensiell kryptoanalyse, lineær kryptoanalyse, og angrep med beslektede nøkler (related key attack).

Blokkchiffer designprinsipper – antall runder

Jo flere antall runder, jo vanskeligere er det å utføre kryptoanalyse. Generelt bør kriteriet være at antallet runder velges slik at kjente kryptoanalytiske metoder krever større innsats enn et enkelt uttømmende nøkkelsøk. Hvis DES hadde hatt 15 eller færre runder, ville differensiell kryptoanalyse krevd mindre innsats enn et uttømmende søk.

Funksjonen F

Hjertet til et Feistel blokk-chiffer er funksjonen F. Dess mer ikke-lineær F er, dess vanskeligere vil enhver form for kryptoanalyse være. Algoritmen bør ha gode skred-egenskaper. Det strikte skred-kriteriet (Strict avalanche criterion – SAC) sier at ethvert output bit j fra en S-boks skal endre seg med en sannsynlighet på 0,5 når ethvert enkelt input bit i endres for alle i , j. Bit uavhengighetskriteriet (BIC) sier at to vilkårlig valgte output bit j og k skal endre seg uavhengig av hverandre når et vilkårlig enkelt input bit i  endres for alle i , j , og k. Disse to kriteriene (SAC og BIC) later til å styrke effektiviteten til forvirringsfunksjonen (confusion function).

Nøkkelplanalgoritme

Ved ethvert Feistel blokkchiffer brukes nøkkelen til å generere en subnøkkel i hver runde. Generelt ønsker vi å velge subnøkler som maksimaliserer vanskeligheten av å dedusere individuelle subnøkler, samt gjør det vanskelig å jobbe seg tilbake til den fulle nøkkelen. Det foreslås, som et minimum, at nøkkelplanen bør garantere SAC og BIC for nøkkel og klartekst.

Photo by Ibrahim Boran from Pexels