Dagens tekst er hentet fra kapittel 7 i Cryptography and Network Security. Dette kapitlet skal se nærmere på hvordan man bruker blokkchiffre i praksis.

Flere krypteringer og DES

Som tidligere nevnt ble det på 90-tallet klart at det var behov for en erstatter for DES; det var teoretisk angrep som kunne knekke DES på kortere tid enn uttømmende søk – og etter hvert ble det mulig å kjøre uttømmende søk i løpet av noen timer. AES ble svaret på dette behovet, men før dette var det et alternativ å foreta flere krypteringer av samme blokken vha. DES-implementasjoner. Triple-DES var den foretrukne varianten her.

Dobbel DES?

Vi kunne forestille oss å bruke to DES-krypteringer på hver blokk, etter formelen C = E_K2(E_K1(P)). En tidlig bekymring her var om dette kunne være ekvivalent med en enkelt kryptering vha. en tredje nøkkel (dette viste seg senere å være ubegrunnet).

Et angrep som møtes på midten

Et virkelig problem er imidlertid det såkalte «møtes-i-midten»-angrepet, som kommer til anvendelse hver gang man bruker et chiffer to ganger, siden X = E_K1(P) = D_K2(C). Angrepet består i å kryptere P med alle mulige nøkler, og lagre resultatet (dvs. 2⁵⁶ mulige verdier for X). Deretter dekrypterer man C med alle nøkler til man finner en match i listen med X-er. Det kan vises at dette tar O(2⁵⁶) steg, som er tilsvarende å knekke vanlig DES. Dette angrepet vil fungere mot alle blokkchiffer som brukes på denne måten.

Triple-DES med to nøkler

Det nærliggende mottrekket til «møtes-i-midten»-angrepet er å bruke tre krypteringstrinn med tre forskjellige nøkler. Dette hever kostnaden av angrepet til 2¹¹², som betyr at det fortsatt ikke lar seg gjøre med dagens teknologi. Ulempen er at det krever en nøkkellengde på 56 x 3 = 168 bits, som ble oppfattet som litt uhåndterlig. Som et alternativ foreslo Tuchman en metode for trippel kryptering som bare bruker to nøkler. 3DES med to nøkler er et relativt populært alternativ til DES, og har blitt tatt i bruk i nøkkelhåndteringsstandardene ANSI X9.17 og ISO 8732.

Vi bruker 2 nøkler med E-D-E sekvensen: C = E_K1(D_K2(E_K1(P))). Kryptering og dekryptering er ekvivalente fra et sikkerhetssynspunkt, og hvis K1=K2 blir resultatet det samme som for vanlig DES. Det er for øyeblikket ingen kjente praktiske angrep på 3DES med to nøkler, men det er flere teoretiske angrep som kan danne basis for praktiske angrep i framtiden.

Triple-DES med tre nøkler

Selv om det ikke er noen kjente praktiske angrep på 2-nøkkel 3DES, er det noen indikasjoner som gir grunn til uro. Mange forskere mener nå at 3-nøkkel 3DES er det foretrukne alternativet; dette gir en effektiv nøkkellengde på 168 bits, og er definert som C = E( K₃, D( K₂, E( K₁,  P))). Tilbakekompatibilitet med DES oppnås ved å sette K₃ = K₂ eller K₁ = K₂. Et antall internett-baserte applikasjoner har tatt i bruk 3-nøkkel 3DES, inkludert PGP og S/MIME.

Operasjonsmodi

Når man bruker en kryptografisk algoritme på en bestemt måte for å forbedre effekten eller tilpasse den en spesiell applikasjon, kaller man dette for en operasjonsmodus. NIST har definert fem bestemte operasjonsmodi for blokkchiffer som er ment å dekke et bredt spekter av krypteringsanvendelser hvor et blokkchiffer kunne brukes. Disse modiene er ment for bruk med ethvert blokkchiffer, inkludert 3DES.

Elektronisk kodebok (ECB)

Meldingen brytes opp i uavhengige blokker som krypteres hver for seg uavhengig av andre blokker. Hver blokk er en verdi som erstattes av en annen verdi; herav navnet. C_i = E_K(P_i)

ECB kan egentlig bare brukes for å sende enkeltverdier på en blokkstørrelse eller mindre. Hvis man bruker ECB til å kryptere en større datamengder, kan repetisjoner internt i dataene (tekst, bilde, …) vise igjen i chifferteksten, dersom repetisjonene faller sammen med blokk-grensene. Dette gjelder spesielt med data som bildefiler, eller meldinger som endrer seg veldig lite; dette reduseres da til kodebok-analyse. Svakheten skyldes det at de krypterte meldingsblokkene er uavhengige.

Kriterier for bedre alternativer til ECB

Ettersom ECB ikke er godt nok for større datamengder, må vi finne på noe bedre. Følgende kriterier må tas hensyn til når man skal finne en ny operasjonsmodus: Overhead, gjenoppretting ved feil, spredning av feil, diffusjon og sikkerhetsnivå.

Cipher Block Chaining (CBC)

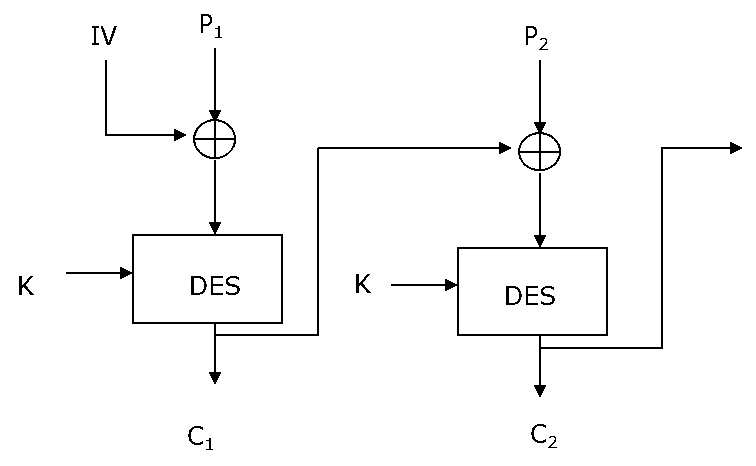
Ved CBC brytes meldinger opp i blokker, og lenkes sammen i krypteringsoperasjonen. Hver foregående blokk lenkes med den nåværende blokken; herav navnet. Vi trenger en tilfeldig valgt initialiaseringsvektor (IV) for å starte prosessen.

C_i = E_K(P_i XOR C_i-1)
C_-1 = IV

CBC kan brukes til å kryptere større mengder data, men kan også brukes som en meldingsautentiseringskode (MAC) – mer om dette i senere kaptitler. (I de følgende figurene er DES brukt som blokkchiffer – men det kan man gjerne bytte ut med AES i våre dager.)

Polstring

På slutten av meldingen må man håndtere tilfellet hvis meldingen ikke fyller opp den siste blokken. I så fall må den siste blokken «polstres» (pad) med en kjent verdi som ikke tolkes som data (f.eks. nuller). Et alternativ er at man polstrer og avslutter med en angivelse av polstringsstørrelsen, f.eks.:
[ b1 b2 b3 0 0 0 0 5] betyr at vi har 3 data bytes, og så 5 bytes polstring+teller. I enkelte tilfeller vil dett kreve at man sender en hel ekstra blokk bare med polstring. Det finnes andre modi for spesielt interesserte som unngår behovet for en ekstra blokk, men vi går ikke inn på disse her.

Fordeler og ulemper ved CBC

En chiffertekstblokk avhenger av alle foregående blokker, så enhver endring (eller feil) påvirker alle etterfølgende blokker. Man trenger en Initialiseringsvektor (IV) som må være kjent for sender og mottaker. Hvis denne sendes i klartekst, kan en angriper endre bits i den første blokken, og endre bits i IV for å kompensere. Dette medfører at IV enten må være en fast verdi (som i EFTPOS), eller må sendes kryptert vha ECB i forkant av resten av meldingen.

Strømmemodi

Blokkmodi krypterer hele blokker, men av til trenger man å operere på mindre enheter, f.eks. ved sanntidsdata. Da blir det aktuelt å konvertere et blokkchiffer til et flytchiffer, og alternativene er cipher feedback (CFB) modus, output feedback (OFB) modus, og counter (CTR) modus. Det disse modi gjør, er å bruke et blokkchiffer som en slags pseudo-tilfeldig tall (pseudo-random number) generator.

Cipher Feedback Mode (CFB)

For ethvert blokkchiffer, så utføres kryptering på en blokk på b bits. I tilfellet til DES er b = 64, for AES er b = 128. Meldingen behandles som en strøm av bits som legges til det som kommer ut av blokkchifferet. Resultatet mates tilbake til det neste stadiet (herav navnet). Standarden tillater at et vilkårlig antall bit (1,8, 64 eller 128 etc.) mates tilbake; refereres da til som CFB-1, CFB-8, CFB-64, CFB-128 osv. Det er mest effektivt å bruke alle bitene i blokken (64 eller 128 for hhv. DES og AES). C_i = P_i XOR E_K(C_i-1), C_-1 = IV.

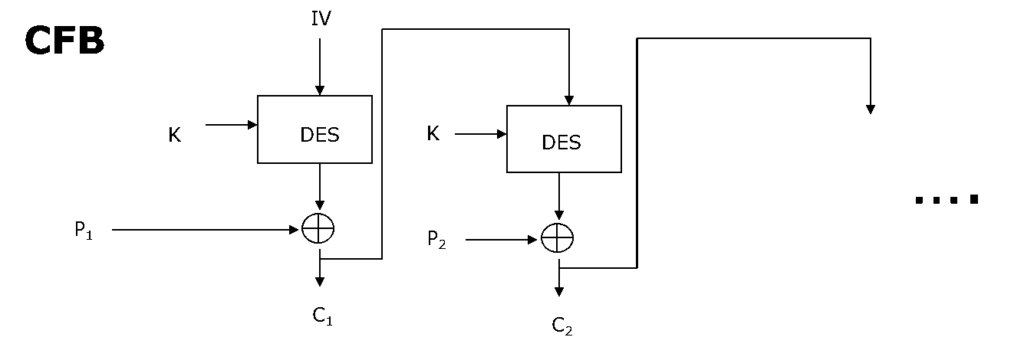
CFB kan brukes for kryptering av datastrømmer og autentisering.

Fordeler og ulemper med CFB

CFP passer bra når data kommer i bits/bytes, og er kanskje den vanligste flyt-modusen. Begrensningen ligger i at flyten potensielt vil stoppe opp hver gang det er behov for å gjøre en krypteringsoperasjon etter hver n bits. Legg merke til at ved CFB brukes chifferet i krypteringsmodus i begge ender. Eventuelle feil propagerer for flere blokker etter feilen.

Output FeedBack (OFB)

I OFB behandles også meldingen som er strøm av bits. Resultatet av krypteringen legges til meldingen, men resultatet (før XOR med meldingen) er også det som mates tilbake til neste runde –  derav navnet Output Feedback Mode. Denne måten å gjør at tilbakematingen er fullstendig uavhengig av meldingen, og vi kan betrakte OFB som en måte å lage en nøkkelstrøm for en one-time pad; denne nøkkelstrømmen kan genereres så lang man bare ønsker på forhånd.

O_i = E_K(O_i-1)

C_i = P_i XOR O_i

O_-1 = IV

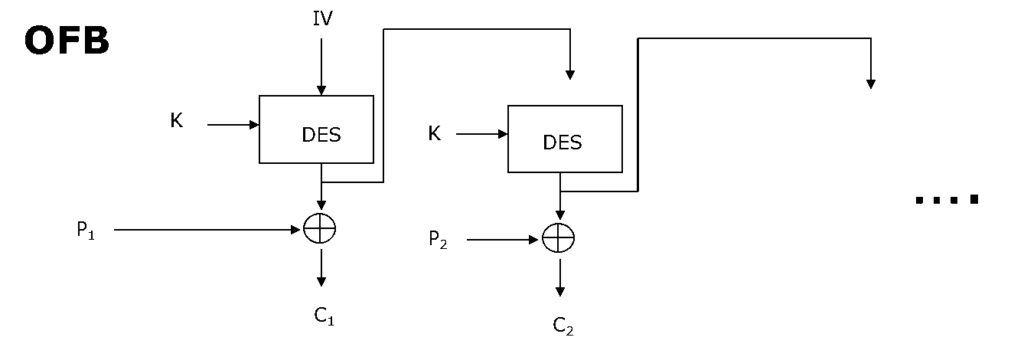
OFB kan brukes til flytkryptering på støyende kanaler.

Fordeler og begrensninger med OFB

OFB trenger en IV som er unik for hver bruk; hvis den noensinne skulle bli gjenbrukt med samme nøkkel vil en angriper kunne finne tilbake til klarteksten – dette er det samme som hvis man skulle bruke en one-time-pad mer enn en gang. Bit-feil forplanter seg ikke, men denne modusen er mer sårbar for modifikasjon av meldingsstrømmen. Sender og mottaker er nødt til å være fullt synkronisert. Senere tids forskning har vist at kun tilbakemating av fulle blokker (dvs. OFB-64 eller OFB-128) bør brukes.

Counter Mode (CTR)

CTR betraktes som en «ny» modus; selv om den var forslått for en del år siden, var den f.eks. ikke med i 2. utgave av Stallings’ lærebok. CTR likner på OFB, men krypterer en tellerverdi i stedet for noen tilbakekobling. Tellerverdien for en gitt nøkkel må aldri gjenbrukes, ettersom det ville resultert i samme one-time-pad.

O_i = E_K(i)

C_i = P_i XOR O_i

OFB kan brukes for høyhastighets nettverkskryptering.

Fordeler og ulemper med CTR

CTR har en stor fordel når det gjelder effektivitet; man kan gjøre parallelle krypteringer i maskinvare eller programvare, og kan også lage nøkkelstrømmen på forhånd (som OFB). Dette gjør CTR et bra valg for høyhastighetsforbindelser der trafikken kommer støtvis. Det er mulig å gjøre tilfeldig oppslag i krypterte blokker, og man kan bevise sikkerhetsnivået (CTR er minst like god som andre modi). Andre fordeler omfatter effektive implementeringer i maskinvare og programvare, og at modusen er veldig enkel å beskrive.

Den store utfordringen med CTR er som nevnt at man aldri må gjenbruke tellerverdien, som nevnt over.

Justerbare blokkchiffre

XTS-AES modusen er basert på konseptet om et justerbart (tweakable) blokkchiffer. Den generelle strukturen er 3 input: Klartekst P, symmetrisk nøkkel K og en justering (tweak) T. Justeringen trenger ikke holdes hemmelig, på samme måte som saltet i enkelte passordløsninger. Hensikten er å sørge for variabilitet.

XTS-AES Mode for Block-Oriented Storage Devices

XTS-AES ble godkjent som en ekstra blokkchiffermodus av NIST i 2010, også standardisert som IEEE Std 1619-2007; denne har fått bred støtte i industrien. Standarden beskriver en metode for å kryptere data som lagres i sektor-baserte enheter hvor trusselmodellen omfatter mulig tilgang til lagrede data av en angriper. Her er det andre krav enn når man sender data over en kommunikasjonskanal.

Krav for kryptering av lagringsmedium

Kravene for kryptering av lagrede data, også kjent som «data i ro», er noe annerledes fra krav til data som skal sendes. P1619 standarden var utviklet for å ha følgende karakteristikker: Chifferteksten er antatt å være fritt tilgjengelig for angriperen. Plasseringen av data endres ikke, verken på lagringsmediet eller i transitt, og data aksesseres i blokker av fast størrelse (16 bytes), uavhengig av hverandre. Det brukes ikke noen andre metadata, unntatt plasseringen av datablokkene i hele datamengden.

Den samme klarteksten krypteres til forskjellige chiffertekster på forskjellige lokasjoner, men alltid til den samme chifferteksten når den skrives til den samme lokasjonen igjen. Det går an å lage en standard-konform enhet som kan dekryptere data som er kryptert av en annen standard-konform enhet.

XTS-AES Operasjon på en enkeltblokk

Bruker AES to ganger for hver blokk: T_j = E_K2(i) ⊗ α^j , C_j = E_K1(P_j ⊕ T_j) ⊕ T_j  – hvor i er justeringen (tweak) og j er sektornummer. Hver sektor kan bestå av flere blokker.

( ⊗ betyr her polynom-multiplisering i GF(2¹²⁸) , ⊕ er vanlig XOR)

Fordeler og begrensninger av XTS-AES

XTS-AES er effektiv; det er mulig å foreta parallelle krypteringer i maskinvare eller programvare. Det er også mulig å få vilkårlig tilgang til datablokker (trenger ikke lese dem i rekkefølge). XTS-AES har både nonce og teller, og adresserer sikkerhetsutfordringer relatert til lagrede data.

Format-Preserving Encryption (FPE)

FPE refererer til enhver krypteringsmetode som tar en klartekst i et gitt format, og produserer en chiffertekst i det samme formatet. For eksempel: Kredittkortnummer består av 16 desimale siffer, og en FPE som kan akseptere denne typen input vil produsere chiffertekst som også er 16 desimale siffer (bemerk at chifferteksten trenger ikke være, og er faktisk sannsynligvis ikke, et gyldig kredittkortnummer – men det vil ha samme formatet og kan lagres på samme måte som et klartekst kredittkortnummer).

Motivasjon

FPE gjør det mulig å ettermontere sikkerhet i eksisterende applikasjoner hvor konvensjonell kryptering muligens ikke lar seg gjøre fordi det ville rote til datafelter eller kommunikasjonsveier. FPE har vist seg å være et nyttig kryptografisk verktøy, med anvendelser som omfatter sikkerhet for finansiell informasjon, data-sanering, og transparent kryptering av innslag i eldre databaser. Hovedfordelen er at FPE gjør det mulig å beskytte bestemte dataelementer, uten å påvirke arbeidsprosesser som eksisterte før FPE var tatt i bruk. Det er ikke nødvendig å gjøre endringer i databaseskjema, og kun minimale endringer i applikasjonene – bare applikasjoner som trenger se klarteksten av et dataelement må modifiseres, og typisk bare mindre endringer.

Noen eksempler på slike gamle (legacy) applikasjoner hvor FPE er ønskelig: COBOL data-prosesseringsapplikasjoner, database applikasjoner. FPE-krypterte tegn kan komprimeres betydelig for effektiv transmisjon.

Utfordringer med å lage en FPE

En generell standardisert FPE bør tilfredsstille et antall krav:

• Chifferteksten må være same lengde og format som klarteksten
• Må kunne tilpasses forskjellige tegn og nummer-typer
• Må fungere med variabel lengde klartekst
• Sikkerhetsstyrke må være tilsvarende til det man får med AES
• Sikkerheten må være høy selv for veldig små lengder klartekst.

Eksempel: Streng med desimale siffer med maks lengde 32 siffer. Dette kan representeres ved 16 bytes (128 bits), hvor vi koder hvert siffer med 4 bit (dvs. 6 kodes som 0101). Klartekst input X = 128-bit binær streng av 4-bit desimale siffer X[1] . . . X[16], hvor vi polstrer mot venstre (mest signifikant) med nuller hvis vi har færre enn 32 siffer. Med nøkkel K, chiffertekst Y = AES_K(X) er en string av lengde 16 av 4-bit par. (Her er det en liten feil i boken, og det som følger er kanskje litt grisete, men heng på). For enkel regning lager vi oss en midlertidig tabell A[32], hvor vi splitter parene; slik at A[i] = 0x00FF * Y[i] og A[i+16] = (0xFF00 * Y[i])>>4. Nå vil enkelte av innslagene i A være > 9 (f.eks. 1100), så for å lage chiffertekst Z i det ønskede formatet må vi beregne: Z[i] = A[i] mod 10 + (A[16+i] mod 10)<<4,  for 1 ≤ i ≤ 16. Her får vi imidlertid ingen reversibilitet; det blir en mange-til-en funksjon, f.eks. er 12 mod 10  =  2 mod 10  =  2.

16-siffer kredittkortnummer (CCN)

De første 6 sifrene i et kredittkortnummer identifiserer utstederen av kortet (IIN), det siste sifferet er en enkel sjekksum for å detektere pølsefingre eller andre feil, og de gjenværende 9 sifrene er kundens kontonummer. De siste fire sifrene vises ofte i klartekst for å dobbeltsjekke kvitteringer etc.  – dette gir oss bare 6 siffer vi kan kryptere. Vi kunne brukt et justerbart (tweakable) blokkchiffer, hvor justeringen for kredittkortnumre kunne være de første to og de siste fire sifrene av CCN.

Strenger av tegn

NIST og andre FPE-algoritmer som har blitt foreslått brukes med klartekst som består av en streng av elementer som vi kaller tegn. En endelig mengde med to eller flere symboler kalles et alfabet. Elementene i et alfabet kalles tegn. En teg.streng er en endelig sekvens av tegn fra et alfabet. Individuelle tegn kan repeteres i strengen. Antallet forskjellige tegn i et alfabet kalles basen (eller radix) av alfabetet.

NIST Metoder for Format-bevarende kryptering (FPE)

De tre metodene FF1, FF2, og FF3 bruker alle Feistel-strukturen i Figur 7.12 (se boken), men bruker noe forskjellige rundefunksjoner F_K, som lages med AES.

Viktige forskjeller: FF1 støtter den største variasjonen av lengder for klarteksten og justeringene, rundefunksjonen bruker en cipher-block-chaining (CBC) type kryptering, mens FF2 og FF3 bruker en simpel elektronisk kodebok (ECB) kryptering. FF2 bruker en subnøkkel generert fra krypteringsnøkkelen og justeringen, mens FF1 og FF3 bruker krypteringsnøkkelen direkte. Bruk av en subnøkkel kan bidra til å beskytte den opprinnelige nøkkel mot sidekanal analyse (dvs. et angrep som baserer seg på informasjon fra den fysiske implementasjonen av et kryptosystem, snarere enn uttømmende søk eller kryptoanalyse, f.eks. basert på effektbruk eller tidsbruk). FF3 tilbyr det laveste rundetallet, åtte, sammenlignet med ti for FF1 og FF2, og er den minst fleksible mht. justeringene den støtter.

 

Illustrasjon ved Magda Ehlers from Pexels

 

 

 

 

 

 

 

Illustrasjon ved Magda Ehlers from Pexels